Velocities

Barycentric velocity calculation

iSpec incorporates an option for calculating the earth's velocity towards the earth ("Parameters - Calculate barycentric velocity" menu, algorithm based on Stumpff 1980) so that the spectra can be corrected and transformed to the solar barycentric reference frame ("Operations - Correct - Barycentric velocity" menu). For the determination it is necessary to know the date/time of the observation and the star's coordinates (RA: Right Ascension in hours, DEC: Declination in degrees) in epoch J2000.0.

Barycentric velocity determination and correction Barycentric velocity determination and correction

Radial/barycentric velocity determination

The velocity profile can be determined relative to three different references:

  • Atomic data: Useful for determining the radial velocity of a star, considering that the barycentric velocity due to the earth orbit has been already corrected.
  • Telluric lines: It can be used to identify the position of the telluric lines (thus these regions can be ignored) or to evaluate if a given spectrum has already been corrected by the barycentric velocity (if not, the output velocity will be zero).
  • Template: Any loaded spectrum or an internal synthetic one can be used for determining the relative radial velocity.

Velocity determination by using atomic/telluric lines or a template Velocity determination by using atomic/telluric lines or a template Velocity determination by using atomic/telluric lines or a template

The generation of the velocity profile is done by an implementation of the cross-match correlation algorithm which sum up the spectrum's fluxes (f) multipled by a template function 'p':

\[ C(v) = \sum_{lines}\sum_{pix} p(pix, v) \cdot flux(pix) \]

  1. Calculate \(C(v)\) where \(p(pix, v)\) is varied from a lower to an upper velocity in fixed steps.
  2. Normalize \(C(v)\)

The 'p' function represents the fraction of the line of a template spectrum (which depends on the spectral type of the star) that falls on a given pixel at a given velocity.

The cross-correlation can be computed in Fourier space, taking advantage of the correlation theorem although, when the spectrum has a large wavelength, the computation can take more time compare to the normal cross-correlation.

iSpec includes an internal template (it can be found in the directory "input/spectra/synthetic/") which corresponds to a synthetic spectrum of a star with Teff 5777.0, gravity (logg) 4.44 and metallicity 0.02 (solar type) which has been generated by using SPECTRUM, atomic data extracted from the VALD database (350 to 11000 nm) and MARCS model atmospheres. In case that another ground-base observed spectrum is used as template, it is recommended to clean the regions that may be affected by telluric lines.

In the case of selecting the option of using atomic lines, a mask is used instead of a template which means that the 'p' function has values only on the peak of the line and the value corresponds to the depth of the line. The possible masks line lists are:

  • Narval Sun: lines and depths detected from observed asteroids by the NARVAL spectrograph with a wavelength range from 370 to 1048 nm.
  • Solar and Arcuturs atlas: lines and depths detected in the solar and arcturus atlas with a wavelength range from 372 to 926 nm.
  • HARPS/SOPHIE A0, F0, G2, K0, K5, M5: mask specially prepared to be used by HARPS/SOPHIE with a wavelength range from around 375 to 680 nm.
  • Synthetic Sun: lines and depths detected from a synthetic spectrum generated with SPECTRUM, VALD linelist and MARCS model atmosphere with a wavelength range from 350 to 1100 nm.
  • VALD: mask based on a line list extracted from the VALD database with a wavelength range from 300 to 1100 nm. The depth of each line correspond to a star with Teff 5770.0 and gravity (logg) 4.40 (solar type).

For the telluric lines, the mask has been generated from the analysis of a synthetic spectra of the typical telluric lines obtained from TAPAS (an on-line service that provides simulated atmospheric transmission spectra for specific observing conditions).

Internally, for the cross-correlation process, iSpec creates a mask from the given line list with a user defined size. If one or more mask lines fall into one range, the max depth is assigned as the mask value (otherwise it will be zero).

Afterwards, it re-samples the mask uniformly in terms of velocity by using the specified velocity step (recommended to be half of the mask size). This implies that the distance between the elements in the mask is variable in wavelength but constant in velocity (depends on the mask size specified by the user).

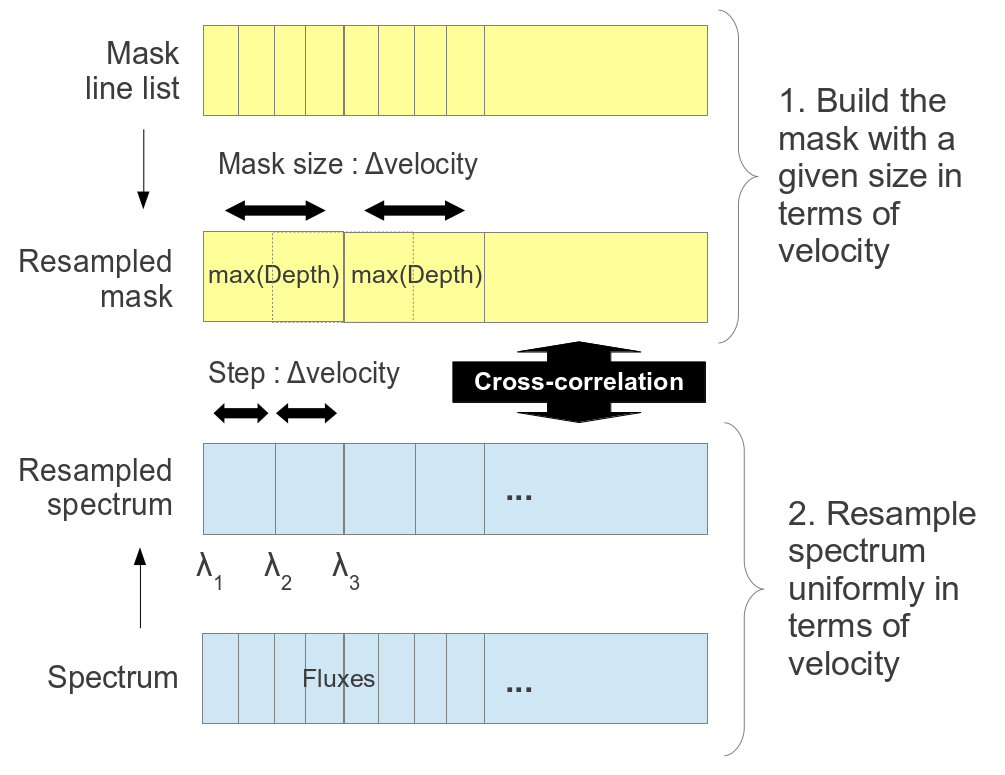
Mask for cross-correlation. iSpec permits to choose the mask size in velocity and the minimum depth

The following formula is used for determining the wavelength ranges:

\[ \lambda_{i+1} = \lambda_{i} + \lambda_{i} \left(1 - \sqrt{\frac{1-\frac{velocity}{c}}{1+\frac{velocity}{c}}}\right)\]

After the mask construction, the spectrum is re-sampled to have the same points as the mask and the cross-correlation algorithm can be easily applied by shifting the mask values to the left/right (each shift represents a constant increment/decrement in velocity). This approach allows to reduce the computation time needed for calculating the velocity respect to the atomic/telluric mask.

The results are presented in a new window where the velocity profile is shown. The mean velocity is calculated by fitting a second order polynomial near the peak and additionally a Gaussian/Voigt is fitted (with fixed mean velocity) to determine other complementary parameters:

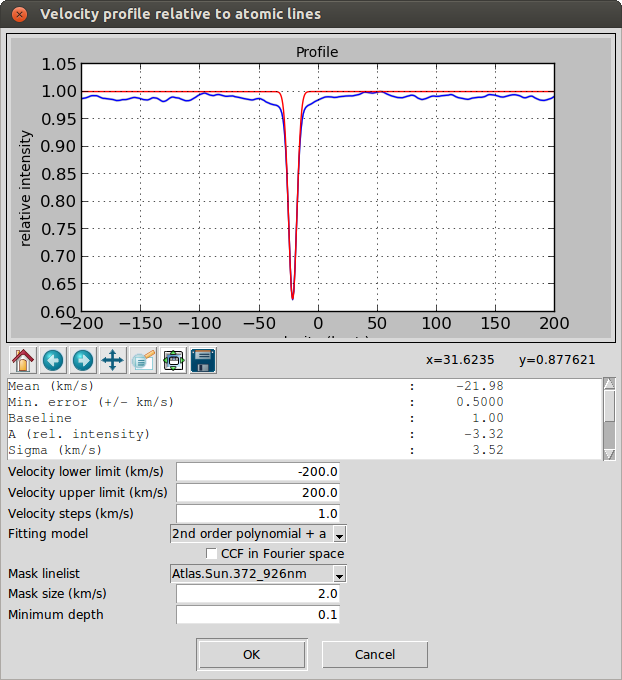
Velocity profile

The error in the radial velocity is calculated following Zucker 2003:

\[ \sigma_{\mathrm{v}}^{2} = - \left[ N \frac{C^{\prime\prime}(\mathrm{v})}{C(\mathrm{v})} \frac{C^{2}(\mathrm{v})}{1 - C^{2}(\mathrm{v})} \right]^{-1} \mathrm{,}\]

where \(N\) is the number of bins in the spectrum, \(C\) is the cross-correlation function and \(C^{\prime\prime}\) is its second derivative.

Radial/barycentric velocity correction

The spectrum and the regions can be shifted considering the determined velocity (or indicating a custom one) by using the option "Operations - Correct velocity...". The following formula is applied:

\[ \lambda_{corrected} = \lambda \sqrt{\frac{1-\frac{velocity}{c}}{1-\frac{velocity}{c}}}\]

where \(c\) is the speed of light in vacuum and \(\lambda\) the original wavelengths.

Spectroscopic binaries identification

The velocity determination function relative to atomic data can be used to identify spectroscopic binaries. In those cases, the resulting profile would have two different peaks:

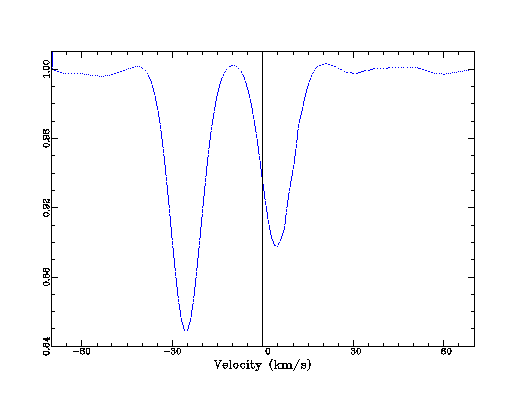
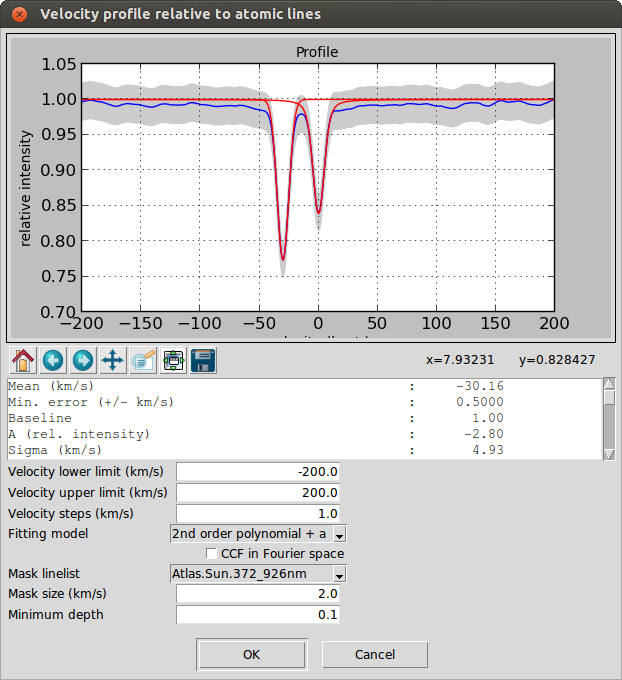
Cross-match correlation determined by ELODIE and iSpec for HD005516A spectroscopic binary Cross-match correlation determined by ELODIE and iSpec for HD005516A spectroscopic binary

As an example, iSpec includes (in the "input/spectra/binaries/" directory) the spectrum of HD005516A observed with ELODIE

  • Date 4.10.1996 / RA 00 57 12.40 / DEC +23 25 03.54
  • ELODIE:
    • RV component 1: -25.49 km/s
    • RV component 2: 4.72 km/s
  • iSpec results with parameters by default:
    • Barycentric vel: 5.15 km/s
    • RV component 1: -30.16 km/s
    • RV component 2: -0.04 km/s
    • RV corrected component 1: -25.01 km/s
    • RV corrected component 2: 5.11 km/s

iSpec will try to automatically detect outliers peaks in the velocity profile in order to detect spectroscopic binaries and fit more than one Gaussian/Voigt.